Making the main game loop

Now that everything is set up, it’s time to get into the actual game. The flow here is processing input first, and then acting based on the received inputs.

GameLoop::
@{Handle joypad input}
@{Handle ball physics}
@{Update screen}
@{Wait one frame}
    jp GameLoop

I wait for one frame to pass first (so as to run the loop once per frame), and then return to the start of the loop. If I didn’t wait a frame first, then the loop would run like a billion times per frame and be actually unplayable, which isn’t what I want.

1. Updating the screen

Stepping one frame at a time

The first thing I’ll do in the game’s main loop is to make sure that the logic is run once per frame. This halt instruction will wait until an interrupt is encountered, and then it’ll resume executing. Since I have VBlank enabled at this point, this is an advantage. Using halt over waiting for VBlank myself saves battery since the Game Boy doesn’t have to keep checking all the time if VBlank is reached or not.

The downside however, is that there’s a hardware bug which sometimes causes the instruction after halt to be executed twice. I’ll place a nop below just to be safe, so that if it happens the Game Boy will do nothing (twice).

    halt
    nop

But since halt waits for any interrupt, it might be a good idea at this point to specifically ask for VBlank, in case I add any more interrupt handlers. I’ll do this by having a flag that will be acknowledged when the VBlank interrupt is encountered.

hAskVBlank:: db

It’s acknowledged by zeroing it out:

    xor a
    ldh [hAskVBlank], a

Now I’ll create a function that specifically waits for VBlank. It sets hAskVBlank and checks if it has been acknowledged.

DelayFrame::
    ld a, 1
    ldh [hAskVBlank], a
.loop
    halt
    nop
    ldh a, [hAskVBlank]
    and a
    ret z  ; exit if vblank is acknowledged
    jr .loop

@{DelayFrame}

And then I’ll replace this frame-waiting code with a single call to the new function:

    call DelayFrame

Updating the sprites

Sprite updating is done from within the game logic. I’ll just reuse the sprite setup routines from earlier, since it’s easier for me to just reinitialize the sprites rather than manually changing their positions one by one.

@{Update sprite positions}

    call SetupLeftPaddle
    call SetupRightPaddle
    call SetupBall

Updating the score display

I could try to make this update within the main loop, because it is possible to update VRAM outside of VBlank. However that requires a wait until the VRAM is writable for each operation, and that may be a bit risky. So, I want to just do it in VBlank instead.

@{Update the score display}

I’ll throw in some more constants to set the starting point of the scores within the tilemap.

LEFT_SCORE_VRAM_START equ $9846
RIGHT_SCORE_VRAM_START equ $984C

ShowScore is going to just use A and HL for the input.

    ld a, [wLeftScore]
    ld hl, LEFT_SCORE_VRAM_START
    call ShowScore
    
    ld a, [wRightScore]
    ld hl, RIGHT_SCORE_VRAM_START
    call ShowScore

And ShowScore is defined… here:

;;--
;; 
;; @param A     score value, BCD
;; @param HL    where in VRAM to place it in
;; 
;; @clobber BC  the split score value
;; @clobber DE  $20 - 1
;;--
ShowScore::
@{Split score into two numbers}
@{Print top half of the score}
@{Print bottom half of the score}
    ret

@{ShowScore}

I’m going to assume that the scoring system operates on binary-coded decimal (BCD). Practically speaking, it just means that the two halves of the score’s hexadecimal representation never go past 9, so no A, B, C, D, E, or F. Sure, the number won’t accurately represent the score as data, but in the interest of making an “easy” implementation, it’ll do.

First I’ll split the number into two parts, and then add them to the starting tile of the numeral “0” in the tileset.

    ld b, a  ; save original number

; get the lower half and put it into C
    and %00001111
    add $10 ; starting tile of numeral "0"
    ld c, a

; get the upper half and put it into B
    ld a, b
    and %11110000
    swap a  ; make it the lower half
    add $10 ; starting tile of numeral "0"
    ld b, a

The score’s “tens” position is now in B, while the “ones” are in C. All that’s left to do is to put them in memory.

    ld [hl], b
    inc hl
    ld [hl], c

I’ll have to move the cursor down, then write the lower half. I’ll add to BC by $10, since the lower half of the numbers in the tile set comes right after the upper half.

; move VRAM position
    ld de, $20 - 1
    add hl, de

; I assume the lower half comes directly
; after the upper half, so add the offset
; to b and c
    ld a, 10
    add b
    ld b, a
    ld a, 10
    add c
    ld c, a

; put it to the screen
    ld [hl], b
    inc hl
    ld [hl], c

2. First visuals

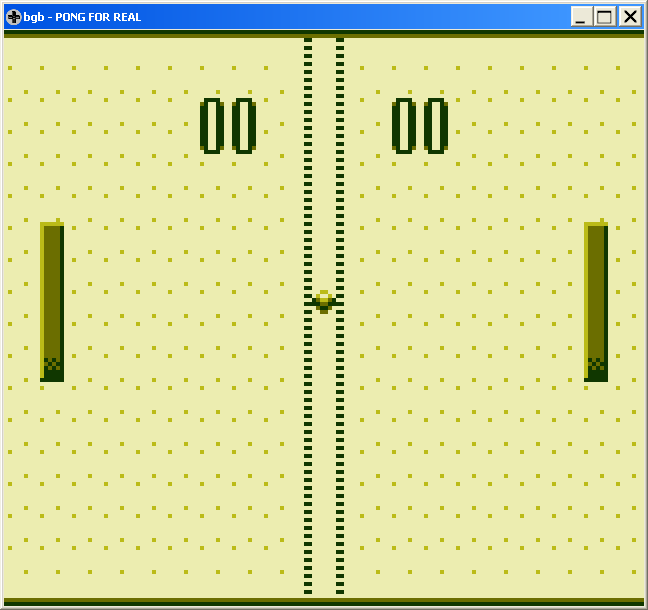
So far, I should have a static screen of just the game objects, the background, and the scoreboard.

If I fiddle around with the memory locations of the paddle positions and whatnot, I can move them “interactively”. A good sign. That means I can just fiddle around with these locations within game code, which I’ll do next.

3. Input handling

The player’s controller should be able to control the paddles. My plan here is to have the player control the left paddle, while the right paddle is a CPU opponent.

So I’ll build the input handling routine thus:

@{Handle the left paddle}
@{Handle the right paddle}

Joypad routine

I’ll need a way to read the Game Boy’s button inputs and store them somewhere to be referred later. I’ll place the destination address to HRAM:

hInput:: db

And an outline of the function to be written:

ReadJoypad::
    @{Read d-pad input and store}
    @{Read button input and store}
    @{Reset the joypad register}
    ret

@{ReadJoypad}

The d-pad input and button input are treated separately by rJOYP, as can be seen from the docs.

The explanation says writing 0 to P14/P15 will select the appropriate button set, but really is writing a 1 into the opposite of the selected button set.

So I make flag constants to reflect this.

F_rJOYP_SELECT_NOT_DPAD    equ 4
F_rJOYP_SELECT_NOT_BUTTONS equ 5

First I select the d-pad (that is to say, “not buttons”). It sets up this register to listen for d-pad inputs.

ld a, 1 << F_rJOYP_SELECT_NOT_BUTTONS
ldh [rJOYP], a

Then I read the input several times, because analog controls are funny. This allows the inputs to stabilize.

rept 4
ldh a, [rJOYP]
endr

The result is stored where everything is 1 except the bits for which the corresponding buttons were set. I want to see a 1 where the button is pressed, so I inverted the result, grabbed only the lower half and swapping it with the upper half, then store temporarily.

cpl       ; flip all the bits
and %1111 ; get only lower half
swap a    ; make it the upper half
ld b, a   ; store to b

Doing the same to the button inputs.

ld a, 1 << F_rJOYP_SELECT_NOT_DPAD
ldh [rJOYP], a
rept 4
ldh a, [rJOYP]
endr

This time, I get to OR it with the value I saved earlier.

cpl              ; flip all the bits
and %1111        ; get only lower half
or b             ; merge with the d-pad input earlier
ldh [hInput], a  ; save

I don’t need to manipulate the joypad anymore, so I’ll try resetting rJOYP.

ld a, 1 << F_rJOYP_SELECT_NOT_BUTTONS | (1 << F_rJOYP_SELECT_NOT_DPAD)
ldh [rJOYP], a

Define joypad constants

The subroutine above places the d-pad set in the upper half (bits 4-7), and the buttons set in the lower half (bits 0-3). hInput can be checked with e.g. the bit <N>, a instruction to see if a certain button is pressed. Let’s define the button flag numbers here:

BUTTONF_A      equ 0
BUTTONF_B      equ 1
BUTTONF_SELECT equ 2
BUTTONF_START  equ 3
BUTTONF_RIGHT  equ 4
BUTTONF_LEFT   equ 5
BUTTONF_UP     equ 6
BUTTONF_DOWN   equ 7

Just in case I’ll want to check a specific button combination, I’ll define its numerical equivalents as well:

BUTTON_A      equ 1<<BUTTONF_A
BUTTON_B      equ 1<<BUTTONF_B
BUTTON_SELECT equ 1<<BUTTONF_SELECT
BUTTON_START  equ 1<<BUTTONF_START
BUTTON_RIGHT  equ 1<<BUTTONF_RIGHT
BUTTON_LEFT   equ 1<<BUTTONF_LEFT
BUTTON_UP     equ 1<<BUTTONF_UP
BUTTON_DOWN   equ 1<<BUTTONF_DOWN

Handle the left paddle

Pong controls are simple—move paddles up and down. Since this will be run once every frame, I check the joypad via the routine from earlier and then jump depending whether the up or down button is pressed. I’m using a compare here because I want to check if only up or only down is pressed, but not both (even though that will resolve to “up” anyway, since up is processed first).

This section could be read as having early ret, except the ret is replaced with a jump to the next section of the code here.

.left_paddle
    call ReadJoypad
    ldh a, [hInput]
    jr z, .left_paddle_done
    
    cp BUTTON_UP
    jr z, .up
    
    cp BUTTON_DOWN
    jr z, .down
    
    jr .left_paddle_done

.up
@{Move the left paddle up}

.down
@{Move the left paddle down}

.left_paddle_done

I define some constants for the paddle’s speed (this is currently static; used in the rept directive), and the upper and lower boundaries where the paddle can’t move any further.

; this is a static constant
PADDLE_SPEED equ 2

; Y boundaries
PADDLES_UPPER_BOUNDARY equ $18
PADDLES_LOWER_BOUNDARY equ $70

Moving the paddle up is basically decrementing wLeftPaddleY (since the value encodes how far down the screen it is) with a check to cap it at the desired boundaries.

    ld a, [wLeftPaddleY]

    rept PADDLE_SPEED
    dec a
    endr
    
    cp PADDLES_UPPER_BOUNDARY
    jr nc, .apply_up

; cap position
    ld a, PADDLES_UPPER_BOUNDARY

.apply_up
    ld [wLeftPaddleY], a
    jr .left_paddle_done

Same with moving it down, except it increments instead.

    ld a, [wLeftPaddleY]
    
    rept PADDLE_SPEED
    inc a
    endr
    
    cp PADDLES_LOWER_BOUNDARY
    jr c, .apply_down

; cap position
    ld a, PADDLES_LOWER_BOUNDARY

.apply_down
    ld [wLeftPaddleY], a
    jr .left_paddle_done

Handle the right paddle

Since the right paddle isn’t going to be controlled by the player, I’ll leave this empty for now.

.right_paddle

Split into subroutines

Okay, so it turns out that I might want to split these into subroutines, after all. Sure, splitting it and then calling them is a bit slower than just placing the code directly, but it helps with readability.

    call HandleLeftPaddleInput
    call HandleRightPaddleInput

Remember when I said about early ret earlier in this page? I turned it into a real-deal early ret:

HandleLeftPaddleInput::
@{Handle the left paddle}
    ret

HandleRightPaddleInput::
@{Handle the right paddle}
    ret

Effectively, this means the jr z, .done instructions (and similar) within those functions can be optimized away to a ret z. But I’m not doing that here, because this markup system as it is would make me rewrite entire sections for that…

4. Ball physics

Well, I’ll try. The ball will be moving at a single speed value, so I’ll have the game try to determine the ball’s next direction and then apply that “vector” to the ball. It’s similar to how the input handling works, really.

    call DetermineBallDirection
    call ApplyBallMovement

DetermineBallDirection::
@{Determine ball's next movement}
    ret

ApplyBallMovement::
@{Apply ball movement}
    ret

I’ll want to keep track of the ball’s direction. Uses three bits: one for the horizontal direction, another for the vertical, and an extra one just because I wanted the ball to start serving straight in the direction of the paddles.

;;--
;; bit 0: left (0) / right (1)
;; bit 1: up (0) / down (1)
;; bit 2: no vertical momentum (0) / vertical momentum (1)
;;--
wBallNextDirection:: db

And the matching flag constants.

; wBallNextDirection bits
F_HORIZONTAL equ 0
F_VERTICAL   equ 1
F_APPLY_VERTICAL equ 2

I’ll first write up the game applying the determined direction, since that’s the easier bit.

@{Apply horizontal movement}

.apply_ball_y
@{Apply vertical movement}

.finished_applying

Determining the direction itself is a bit more involved, since that’s basically the collision checking routine. Instead of checking if the ball is touching another sprite, I want to use hard ranges.

The ball will bounce in both the X and Y directions when it hits a paddle, but only in the Y direction when it hits a wall.

@{Determine if the ball collides with anything}

.switch_directions
@{Switch ball directions}
    jr .skip_collision

.switch_only_y_direction
@{Switch ball directions but only the Y axis}

.skip_collision

Apply horizontal movement

First, let’s deal with how the ball moves horizontally.

@{Determine the ball's new horizontal direction}

.move_ball_right
@{Move the ball to the right}
    jr .apply_ball_y

.move_ball_left
@{Move the ball to the left}
    ; jr .apply_ball_y

I get the next ball’s next direction and store it in B, because I’ll change A a bunch in the following sections. That way I can reuse the original value should A be changed.

    ld a, [wBallNextDirection]
; store next direction in b
    ld b, a
; load horizontal position
    ld hl, wBallX
    bit F_HORIZONTAL, b
    jr z, .move_ball_left

I pointed HL to wBallX and simply incremented and decremented it directly.

    inc [hl]

    dec [hl]

Apply vertical movement

Next up is the ball’s vertical movement. This is similar to the previous section.

@{Determine the ball's new vertical direction}

.move_ball_down
@{Move the ball down}
    jr .finished_applying

.move_ball_up
@{Move the ball up}
    ; jr .finished_applying

Since there’s a flag to apply the vertical movement, I’ll check for that as well. If that’s not set, it skips processing the vertical movement.

    ld hl, wBallY
    bit F_APPLY_VERTICAL, b
    jr z, .finished_applying
    bit F_VERTICAL, b
    jr z, .move_ball_up

    inc [hl]

    dec [hl]

Collision checking

Well, time for the collision check. I’ll first check if the ball hits any of the paddles' X coordinates, and if so, jumps to the paddle collision check portion. I’ll also check if the ball collides with the top and bottom of the arena.

The paddle collision routines are its own little thing here, since the line before it is basically another early return.

@{Check if the ball hits the paddles' X coordinates}
@{Check if the ball is colliding with the top and bottom of the arena}
    jr .skip_collision

.check_left_colliding
@{Check if the ball is touching the left paddle}

.check_right_colliding
@{Check if the ball is touching the right paddle}

Checking if the ball is in the range of the paddles

First I’ll check if it’s in or beyond the line of the left paddle. I’ll add the paddle’s width to the offset because the line to be checked is to the right of the paddle.

I’ll also check if the ball is to the right of where the left paddle begins, that way the ball won’t collide with the space at the back of the paddle.

    ld a, [wBallX]
    cp LEFT_PADDLE_X + PADDLE_WIDTH
    
; [wBallX] <= (LEFT_PADDLE_X + PADDLE_WIDTH)
    jr c, .additional_left_check
    jr z, .additional_left_check
    
    jr .left_x_done

.additional_left_check
    cp LEFT_PADDLE_X
; [wBallX] >= (LEFT_PADDLE_X)
    jr nc, .check_left_colliding

.left_x_done

Then I’ll check if it’s in or beyond the line of the right paddle. In this case, the line is to the left of the paddle. Likewise with making sure it doesn’t collide with blank space.

    cp RIGHT_PADDLE_X - PADDLE_WIDTH
    
; [wBallX] >= (RIGHT_PADDLE_X - PADDLE_WIDTH)
    jr nc, .additional_right_check
    
    jr .right_x_done

.additional_right_check
    cp RIGHT_PADDLE_X + PADDLE_WIDTH
    jr c, .check_right_colliding

.right_x_done

The paddle’s graphics are 1 tile wide, and 1 tile is 8 pixels wide. So:

PADDLE_WIDTH equ 8 ; pixels

Simple paddle collision

Now, I’ve checked that the ball is in the paddle’s horizontal range. Let’s say it passes. I’ll now have to check the vertical range, because the paddles aren’t of infinite height unlike some games I can mention.

I want this to collide when (wLeftPaddleY ≤ wBallY ≤ wLeftPaddleY + PADDLE_HEIGHT).

That is, to say: ((wLeftPaddleY ≤ wBallY) AND (wBallY ≤ wLeftPaddleY + PADDLE_HEIGHT)).

But checking this way would be tricky, so I can invert this to make the ball pass through when: ((wBallY < wLeftPaddleY) OR (wBallY > wLeftPaddleY + PADDLE_HEIGHT)).

    ld hl, wLeftPaddleY
    ld a, [wBallY]
    cp [hl]
; pass if wBallY < wLeftPaddleY
    jr c, .skip_collision

    sub a, PADDLE_HEIGHT
    cp [hl]
; collide if wBallY-PADDLE_HEIGHT = wLeftPaddleY
    jr z, .switch_directions
; pass if wBallY-PADDLE_HEIGHT > wLeftPaddleY
    jr nc, .skip_collision
    jr .switch_directions

I wanted to reuse the value of wBallY somehow, so I expressed that right half as (wBallY-PADDLE_HEIGHT > wLeftPaddleY).

While I’m at it, I’ll define the paddle height here, too. The paddle is 5 tiles tall, so 8 × 5 = 40 pixels…

PADDLE_HEIGHT equ 40 ; pixels

Adding directional awareness

That simple approach creates a bit of a problem where the direction will just be inverted no matter where the ball collided with the paddle. For example, the ball can bounce down even when it collided with the top of the paddle. Probably not what you’ll expect of a standard Pong game.

I’ll want to store how far the ball is from the top of the paddle. That way, the ball will bounce down only when it hits the bottom half of the paddle. Otherwise, it bounces up.

wDeltaYFromPaddle:: db

Then I’ll need to rework the previous logic to reflect this. I changed the first cp [hl] to sub [hl] to get the distance between the top of the paddle and the ball.

There’s also no need to check against [HL] again, since I’m working off of the calculated distance value.

    ld hl, wLeftPaddleY
    ld a, [wBallY]
    sub [hl]
; pass if wBallY < wLeftPaddleY
    jr c, .skip_collision

; pass if wBallY-wLeftPaddleY > PADDLE_HEIGHT
    cp PADDLE_HEIGHT
    jr z, .save_delta_and_collide_left
    jr nc, .skip_collision

.save_delta_and_collide_left
    ld [wDeltaYFromPaddle], a
    jr .switch_directions

Right paddle collision

Now that I’ve got the left paddle collision worked out, it’s a matter of applying the same thing to the right paddle. This is only processed when the ball hits the X position of the right paddle, so wDeltaYFromPaddle should still be correct here.

    ld hl, wRightPaddleY
    ld a, [wBallY]
    sub [hl]
    jr c, .skip_collision
    cp PADDLE_HEIGHT
    jr z, .save_delta_and_collide_right
    jr nc, .skip_collision
.save_delta_and_collide_right
    ld [wDeltaYFromPaddle], a
    jr .switch_directions

Switching directions

Once a collision is detected, I can switch the ball’s direction with respect to the delta Y position previously calculated. At this point, A = wDeltaYFromPaddle, so I don’t need to load it again.

    cp PADDLE_HEIGHT/2
    ld a, [wBallNextDirection]
; bounce down if delta Y > (PADDLE_HEIGHT/2)
    jr nc, .down
; up
    xor a, 1 << F_HORIZONTAL  ; invert the horizontal direction
    res F_VERTICAL, a         ; move up
    jr .set_direction
.down
    xor a, 1 << F_HORIZONTAL  ; invert the horizontal direction
    set F_VERTICAL, a         ; move down
.set_direction
    set F_APPLY_VERTICAL, a   ; always set the vertical apply flag
    ld [wBallNextDirection], a

The xor a, 1 << F_HORIZONTAL instruction couldn’t be placed right after wBallNextDirection was retrieved, since I’d lose the result of the cp PADDLE_HEIGHT/2 instruction. So, that one is duplicated across branches.

Colliding with the bounds of the arena

Fortunately, this is a really simple check.

    ld a, [wBallY]
    cp BALL_UPPER_BOUNDARY
; wBallY < BALL_UPPER_BOUNDARY
    jr c, .switch_only_y_direction
    cp BALL_LOWER_BOUNDARY
; wBallY > BALL_LOWER_BOUNDARY
    jr z, .skip_collision
    jr nc, .switch_only_y_direction

Set the boundaries…

BALL_UPPER_BOUNDARY equ PADDLES_UPPER_BOUNDARY - 8
BALL_LOWER_BOUNDARY equ PADDLES_LOWER_BOUNDARY + (5*8)

…And flip the verticality.

    ld a, [wBallNextDirection]
    xor a, 1 << F_VERTICAL
    set F_APPLY_VERTICAL, a
    ld [wBallNextDirection], a

5. Giving players some points

One way I can give points to the players is by doing it directly when the ball updates its position. So, I’ll modify the ball physics code from before to make it call (or rather—jump to) a scoring function when it hits the edges of the screen.

A point is earned for the left player when the ball goes out on the right half of the screen.

; if new X >= (160+8), score one point towards the left player
    ld a, [hl]
    cp 160+8
    jp nc, ScorePointsAndReset

Likewise, a point earned for the right player when the ball goes out on the left half.

; forcibly clear flags, at this point A=0
    and a  ; clear carry
    rla    ; clear zero

    dec [hl]
    
; if new X < 0, score one point towards the right player
; set carry flag to mark the right player earns 1 point
    jr nz, .apply_ball_y
    scf
    jp ScorePointsAndReset

I’ll use the carry flag to differentiate between the two when going to scoring.

The scoring function

In addition to giving a player 1 point, I want to make it reset the game state so that the next round can begin cleanly.

;;--
;; Score points and reset the game states.
;; 
;; @param Carry   if set, give 1 point to the right player.
;;                otherwise, give 1 point to the left player.
;;--
ScorePointsAndReset::
@{Determine if the score to be given is to the left player or the right}
@{Reset the game state}

.give_point
@{Score points to the appropriate player}

I also want to make it so that the game switches who “serves” the ball. This value will be copied onto wBallNextDirection later.

; wWhichServe values (using wBallNextDirection)
RIGHT_PLAYER_SERVES equ 0
LEFT_PLAYER_SERVES  equ 1 << F_HORIZONTAL

wWhichServe:: db

The target is determined by HL, which is set to the left player’s score’s address initially. When carry is set, it will be overwritten to that of the right player’s. I’ll also want to use this section to set the serving player to that opposite of the winner.

    ld hl, wLeftScore
    jr nc, .left_player_won

; right player won
    ld hl, wRightScore
    ld a, LEFT_PLAYER_SERVES
    ld [wWhichServe], a
    call .give_point
    jr .got_player

.left_player_won
    ld a, RIGHT_PLAYER_SERVES
    ld [wWhichServe], a
    call .give_point

.got_player

And then, reset the game for a new round.

    call ResetGame
    jp GameLoop

Since I’m using BCD for scoring, I’ll be using the decimal adjust (daa) instruction. It relies on the correct flags being set in order to perform the adjustments, so I’m gonna have to reset the flags prior to incrementing it.

    ld a, [hl]
    and a  ; reset flags
    inc a
    daa
    ld [hl], a
    ret

Split off game resetting function

As a consequence, the game initialization routine will have to be split off into its own function. This time, wWhichServe is considered here, and wDeltaYFromPaddle will also be reset.

ResetGame::
    ld a, PADDLES_STARTING_Y
    ld [wLeftPaddleY], a
    ld [wRightPaddleY], a
    
    ld a, BALL_STARTING_X
    ld [wBallX], a
    
    ld a, BALL_STARTING_Y
    ld [wBallY], a
    
    ld a, [wWhichServe]
    ld [wBallNextDirection], a
    
    xor a
    ld [wDeltaYFromPaddle], a
    
    call SetupLeftPaddle
    call SetupRightPaddle
    jp SetupBall

    call ResetGame

@{Score points and reset the game state}
@{ResetGame}

6. The simplest possible AI

As mentioned earlier, I reserved the right paddle handler routine to be controlled as the CPU opponent. I’m gonna attempt to make its “thinking” routine.

First, I’ll make a very simple one that just copies the position of the ball.

.right_paddle
@{Load the ball's current Y position}
@{Set position boundaries}
@{Set right paddle's Y position}

    ld a, [wBallY]

I also apply the boundary checks here.

; assumes A is the calculated paddle position
    cp PADDLES_UPPER_BOUNDARY
    jr c, .limit_upper
    cp PADDLES_LOWER_BOUNDARY
    jr nc, .limit_lower
    jr .set_paddle_y
.limit_upper
    ld a, PADDLES_UPPER_BOUNDARY
    jr .set_paddle_y
.limit_lower
    ld a, PADDLES_LOWER_BOUNDARY
    ;jr .set_paddle_y

.set_paddle_y
    ld [wRightPaddleY], a

What this results in is a pretty unfair AI that always catches the ball. Let’s just say you’ll be having a hard time beating it.

Delayed AI

Let’s make it a bit fairer. How about having the paddle move only after a short while? Say, it should wait a couple of frames until it’s able to move the paddle.

I can do this by setting a single delay and then having a timer that decrements on every step. Then when the timer hits zero, the paddle can move and the timer can be reset again. I’m gonna need two extra variables:

wAIMovementDelay:: db
wAISetDelay:: db

Next, the delay constant.

RIGHT_PADDLE_DELAY equ 1

I set this up in the intializer function.

    ld a, RIGHT_PADDLE_DELAY
    ld [wAISetDelay], a

Next, let’s rework the right paddle function.

.right_paddle
@{Determine if the right paddle can move or not}
@{Only decrement the timer}

.move_paddle
@{Reset the timer}
@{Move the right paddle relative to the ball}

.check_boundaries
@{Set position boundaries}
@{Set right paddle's Y position}

.skip_right_paddle

First up, I’ll check the timer if it’s run out. If so, I can try moving the right paddle.

    ld a, [wAIMovementDelay]
    and a
    jr z, .move_paddle

Otherwise, I’ll just decrement the timer and skip trying to move it.

    dec a
    ld [wAIMovementDelay], a
    jr .skip_right_paddle

If the timer did reach zero, it’ll be reset to its initial value.

    ld a, [wAISetDelay]
    ld [wAIMovementDelay], a

And then move the paddle up or down depending on whether the ball is above the paddle or below the paddle.

    ld hl, wRightPaddleY
    ld a, [wBallY]
    cp [hl]
    ld a, [hl]

; if paddle is lower than ball, move up
    jr c, .move_up

; else, move down
    inc a
    jr .check_boundaries

.move_up
    dec a
    ; jr .check_boundaries

And there you have it, an AI you can beat. Well, there are quirks to be sorted out here, but it’s alright I guess, even though this is more A than I.

7. First proof of concept

With that, I’ve got the first version that’s “playable”. Kinda. For the most part, the basic parts of the game works as expected:

• Controlling the left paddle with the d-pad
• Scoring and beginning a new round
• Ball physics
• CPU player moving the right paddle